(後半にC問題の解説を書きました。Intersection of Two Prismsを解くときとかでも参考にしてください。)
とりあえず書きたいことはたくさんあるんですが、いっぺんに大量に文章を書くのが苦手なのと今日昼過ぎに帰ってきたので体力的にもアレなので、とりあえずWF参加記のうちコンテストに関することだけをここにまとめておきます。*1
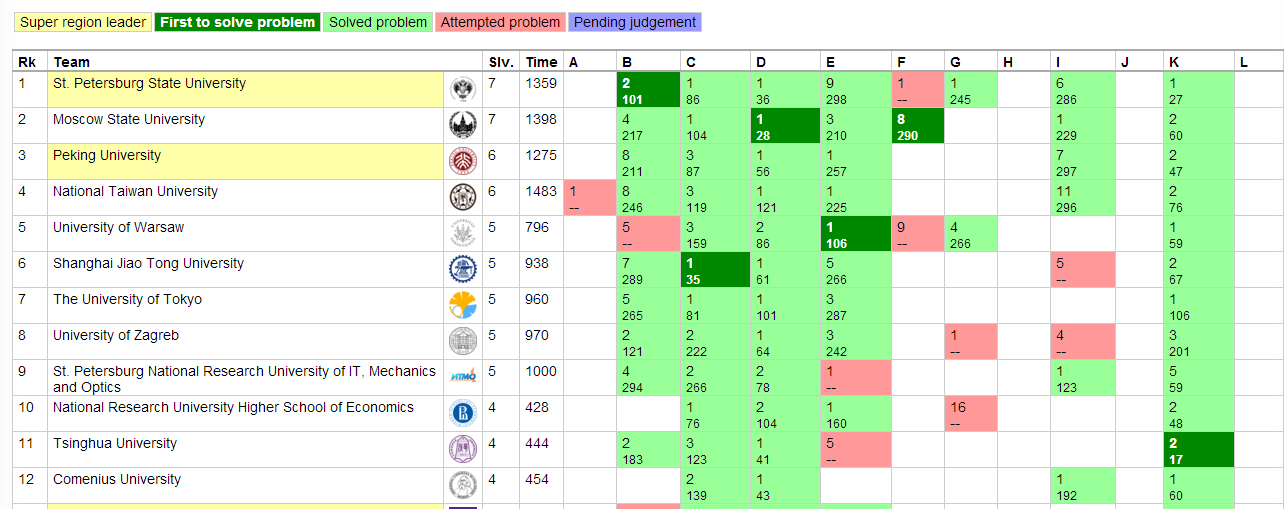
まず結果からいうと、こんな感じでした。(言ってないじゃん、という意見はなしで…)
勝因は対策が嵌りすぎたことと、前半の問題に嵌らなさ過ぎたことだと思います。ということでそこらへんにも触れつつ書き始めてみたいと思います。
ちなみに担当的には僕がC、evimaさんがD,E、skyさんがB,Kでした。
エカテリンブルグに着いてから
Twitterを見ている人は、Quest(あとでこれについては書きます)とかを毎日のようにやって遊びまわっているだけのように見えたかもしれません。というか実際かなり遊びまわっていました。プログラミングをしていたのはついてから2日目(夕方にRegistrationするだけの日)の昼と各自適当に夜、くらいでした(evimaさんは大学の課題に負われて毎日夜中課題をやっていた気がする)
wakabaがWFに来るまでにジャンルを絞ってやった対策はこのくらいしかありません。カッコ内はAOJ-ICPCの点数
- 幾何の対策: ドッグフード(1000)、締まっていこう(1100)、番犬派遣会社(1100)
- 構文解析の対策: Chemist's Math(800)、ASCII Expression(800)、Matrix Calculator(800)
後はそれなりの頻度でチーム練習をしに本郷に行っていました。(週一でやってたのはWF直前2週間くらいだけです)
ということで過去のコンテストでも個人的にも練習会でもぜんぜん見ないor捨てていたジャンルをあわてて対策することにしました。それは
- 数値積分: Intersection of Two Prisms(750)
- 空間幾何: Paperweight(2009 Final K)
- monge DP: 一応簡単なものを理解したり
とはいっても空間幾何なんてすぐにマスターできるようなものでもないので、evimaさんは会場の壁お絵かきゾーンに空間幾何出るなみたいなことを書いていた気がします。というか3人で全く同じジャンルを対策してもしょうがない気もするんですが。
さて、これが上手く嵌りすぎました。コンテスト本番の問題を見ていくことにしましょう。
コンテスト本番の問題
ということで毎日Questをやって結構体力を消費しつつも(前日は1時間近く歩いた)、無事にコンテストを迎えることになりました。問題をぱらっと見た感じの感想はこんな感じ。(問題はhttps://icpc.kattis.com/problemsから閲覧して実際にsubmitすることができます。)
A: パズル系。こういうのは強い人がいるでしょう。
B: 問題文難しい。積分記号が書いてある。DPっぽい。
C: 問題文難しいけど重心をどうにかするらしい。どうみても数値積分だ。
D: ゲーム系。問題文読めない。
E: 意味不明な設定だ。
F: 動く系幾何。こんなの人間が解けるとは思えない。
G: 写真が書いてあるから簡単そう(cf.Матрёшка(2013 Final H))、いや嘘だ、ぜんぜん解けない。
H: アホかよ
I: こういう設定の問題よくみる気がする…あ、Gで見た設定に近いこれは…
J: 図が恐ろしすぎる。
K: 問題文難しい。有名問題に似てるなあ。蟻本だな(確信)
L: 双対っぽいけどやりたくない…。
うろ覚えな時間の流れとともに追っていきます。あとで本番のソースコードが手に入ったらここに貼る予定です。
コンテスト開始
自明枠を探す。ない。ぜんぜん、ない。おかしい…。というか問題文が読めないんだけど…。
17分経過後にKのFAが出る。読んだら有名問題に似てるじゃん。なるほどね。と思う。
でもどうすればいいんだろう…
あ、DのFAも出た。問題文意味不明なのに…。
とりあえずCは数値積分して不等式解くだけだしおととい対策した自分が書くことにする。もうどこが事故るポイントなのかは全部把握しているぞ。
C書き始める。
途中、SJTUがCのFAを取る。やっぱりな。
コンパイル後サンプルが通らないので、印刷して交代。
D,Kの解法も出揃い、2問のソースコードも書く。
Kは蟻本に載っているダブリングのアレだ、となるがevimaさんはダブリングしたことがないらしいのでskyさんが書くことになる。evimaさんはDを書くことにする。ソースコードを紙に書いていた。
C Yes!!
ぜんぜん嵌らずに瞬殺できたつもりでいたが例によって3並列なので81分かかっている。しょうがないね。
とりあえず次に考えるべきはIかGかな~と思い二つの問題を考える。わからん。Aはパズルっぽいしこっちもワンチャンあるな。わからん。
D Yes!!
K Yes!!
順調にいってしまった。問題はここから何も解けるものがないことだ。どうすりゃいいんだ。
しばらく時間が経つも、ぜんぜん思いつかない。
んだけど、4問解いているチームが一向に増えない。やっぱり今回の問題セットは闇だ。
skyさんがBは離散飯のほうでmongeみたいなDPをして連続飯のほうで二分探索すればいいと言う。
確かにそうですね…。やっぱりDPのプロだ…。skyさんがコードを書き始める。
evimaさんはEはkinabaさんがadvent calendarに書いたやつと同じ問題だと言う。
何でそんなの覚えてるんだすげえ(僕は読んでません)。解法説明してもらっても意味不明なのでもう任せることにする。引き続き僕はIを考える。ウム、分からん。無理でしょこれ。
例によってskyさんとevimaさんが交互にデバッグをしつつ、Bをsubmit。WAが生える。
サンプル作っていろいろ試してみたけどそれでも足りないのか。と思ったら罠が大量にあることに気づく。例を挙げるときりがないが、答えが-500000000000位のケースとかは普通に存在することがわかる。やっぱりこのコンテスト闇でした。
Bはいろいろ対策しても通らないので、小さいランダムケースを作って自明DPと比較することにする。Eもコードを書き進める。evimaさんに頼まれてUnion-Findのコードを書いたが、その後怪しげな関数の呼び出しをしていたのを呼び止める。
順位表凍結。
B、闇だ。途中からぜんぜん合わなくなるとか言っていた。skyさんがいろいろなデバッグ出力をして試しているのを眺めていた。なんとか原因が分かり修正することができた。
B Yes!!
もう時間がぜんぜんない。とりあえずEをデバッグだ。
サンプルを何とか通すことができたがWAする。コードを見てみる。なんかnoneまわりが怪しいぞ!?!?!?!?!?
直す。通る。やったぜ。ハイタッチする。
休憩Phase
やり遂げた(自分は1つしかやってないけど)。たぶんメダルは来るだろう。たぶん銀と銅の微妙なところだと思うけど、満足度をf(x)とすると自明にf(銅)-f(メダルなし)>f(金)-f(銀)>f(銀)-f(銅)だよね、という話をしていた。あとマスコットで遊んだり片付けたりしていた。
終了
Tsinghuaが突然叫んだので、抜かれたな、と思った。まあWJMZいるししょうがないか。
結果
A,H,J,Lは誰も解いてなかった。Aは意外だった。
Gが2-SATだとは全く気づかなかった、FA取ったチームは二分探索+2-SAT+フローを定数倍改善したみたいなことを言っていた。
Iは指数時間というのをTwitterで見た。真面目に考えなければよかった。
なんでF解けるの
以上。
自分が解いた問題の解説とか
C - Crane Balancing
(問題文は上のリンクから探して読んでね)

こんな感じで多角形が倒れずにバランスよくおける(y=0の点は二つ以上ある)おもりの重さの範囲を求めてください。
自明な考察
数値積分のポイント (大事)
ということでシンプソン公式で数値積分をするということにしました。
図で例を挙げてこの問題での適用を詳しくみていきます。
まず図形の各頂点のx座標を境に切断面が大きく変わります。ほかのところでは直線的に変化するので、この点での切断面だけ把握すればよいです。

この問題では図形が凸とは限らないので面倒そうに見えますが、一つのx座標においてたくさん図形の線と交わるときは、交点のy座標でソートしてy座標が小さい順にみていったとき、交わるごとに内外が反転するので(y座標偶数番目)-(y座標奇数番目)で幅が求まります。あとはf(x)が1次式なのでxf(x)も2次式にしかならないので、シンプソン公式で正しい積分値が出ます。式変形するとかなり形も単純になって、(b-a)/6*(af(a)+(a+b)(f(a)+f(b))+f(b))とかになるはずです。
さて、ここで罠があります。
一つ目は辺の端点でx座標の切断面と接することがあるということ。これは正直どうとでもなります。
問題はこっちです。

二つの線の両端でかなり切断される長さが変わってしまいます。これにちゃんと気づかないと嵌ります。
ということでx座標列挙をするときにはEPSを足した値、EPSを引いた値両方で代用するのが良いです。片方だけでも嵌ります。
2EPSの幅の積分がどうなろうとほとんど影響がないし、辺と端点で交わるということもなくなるので超便利です。最高。
ということでこれを把握して実装すれば一瞬で終わります。おめでとうございます。